Lecture 9 - Formal Languages, Regular Languages
Thursday, June 19, 2014
5:09 PM
|
|
||||||||||||||||||
|
|
alphabet: finite set Σ of symbols word: finite sequence of symbols over Σ ε: empty string language: set of strings over Σ
Answer: It depends on how complex the language is.
Characterize languages according to how hard the recognition process is: classes of languages based on difficulty of recognition.
Study high-level languages at as easy a class level as possible, move down when we have to.
Finite languages – have only finitely many words
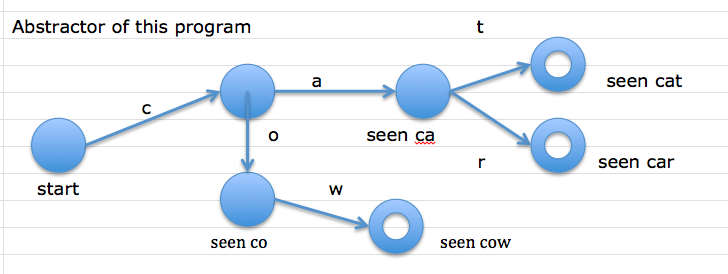
Exercise: L = {cat, car, cow} Write code to answer w ε L, such that: w is scanned exactly once, without storing previously-seen characters.
Bubbles are “states” – configurations of the program based on input seen.
Since programming languages don’t usually admit only finitely many programs, finite languages are not much use.
They are built from:
Union of two languages
concatenation
repetition
Ex: L = {a, b}
Show {a2nb | n >= 0} is regular
Shorthand-Regular Expressions
IDs = [a-zA-Z], ([a-zA-Z0-9_])*
A C program is a sequence of tokens. Each of which comes from a regular language. C ⊆ {valid C tokens}* So, maybe.
Eg {a2nb | n >= 0} |
|||||||||||||||||
|
|
. |
|||||||||||||||||
|
|